LeetCode70-爬楼梯

发表于 | 分类于

题目链接

英文链接：https://leetcode.com/problems/climbing-stairs/

中文链接：https://leetcode-cn.com/problems/climbing-stairs/

题目详述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

1
2
3
4
5
输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

1
2
3
4
5
6
输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

题目详解

斐波那契，运用动态规划即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class LeetCode_00070 {

    public int climbStairs(int n) {
        if (n <= 2) {
            return n;
        }
        int a = 1, b = 2;
        int res = 0;
        for (int i = 3; i <= n; ++i) {
            res = a + b;
            a = b;
            b = res;
        }
        return res;
    }
}

斐波那契数列存在公式，可以运用公式直接计算。

  • f[0] = 0
  • f[1] = 1
  • f[2] = 1
  • f[3] = 2
  • f[n] = f[n - 1] + f[n - 2]

对于以上斐波那契数列，公式如下：

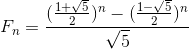
斐波那契公式.gif

对于本题不存在 f[0]，且 f[1] = 1，f[2] = 2，需要将 n 加 1 才能代入公式计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class LeetCode_00070 {

    /**
     * f[0] = 0
     * f[1] = 1
     * f[2] = 1
     * f[3] = 2
     * f[n] = f[n - 1] + f[n - 2]
     * Fibonacci 公式：f[n] = 1 / √5 * {(1 + √5) / 2] ^ n - [(1 - √5) / 2] ^ n}
     * @param n 下标 n
     * @return  f[n]
     */
    public int climbStairs(int n) {
        ++n;    // 调整以运用公式
        double sqrt5 = Math.sqrt(5);
        return (int) ((Math.pow((1 + sqrt5) / 2, n) - Math.pow((1 - sqrt5) / 2, n)) / sqrt5);
    }
}