LeetCode117-填充每个节点的下一个右侧节点指针II

发表于 | 分类于

题目链接

英文链接：https://leetcode.com/problems/populating-next-right-pointers-in-each-node-ii/

中文链接：https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node-ii/

题目详述

给定一个二叉树

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例：

img

1
2
3
4
5
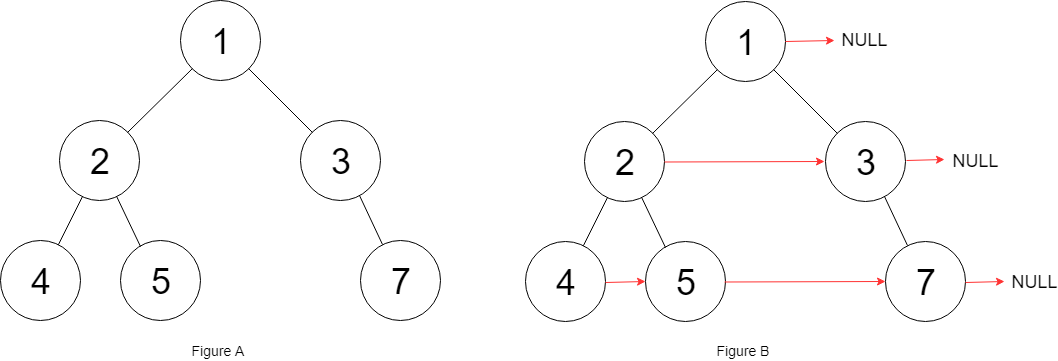
输入：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":null,"next":null,"right":{"$id":"6","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}

输出：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":null,"right":null,"val":7},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"6","left":null,"next":null,"right":{"$ref":"5"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"6"},"val":1}

解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

提示：

  • 你只能使用常量级额外空间。
  • 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

题目详解

本题是 LeetCode116-填充每个节点的下一个右侧节点指针 的进阶版。LeetCode116-填充每个节点的下一个右侧节点指针 给出的树是完美二叉树，而本题不是，属于更普遍的情况。两者思路是一致的，都是从根结点开始进行层次遍历，只不过在连接下一层结点时有所不同。

  • 从根节点开始进行广度优先搜索，每次遍历一层结点。
  • 遍历时维护下一层结点的链表。对于每个结点，依次判断它的左孩子和右孩子是否存在。如果存在，则添加到链表的末尾。为了方便操作，新建一个 dummy 结点作为头结点。
  • 每当遍历完这一层时，代表下一层的结点已经通过 next 指针链接起来了。进入下一层就可以重复这样操作。
  • 由于 next 指针的存在，可以只使用常量级额外空间来进行搜索，空间复杂度为 O(1)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class LeetCode_00117 {

    public Node connect(Node root) {
        Node cur = root;
        while (cur != null) {
            Node dummy = new Node();
            Node tail = dummy;
            while (cur != null) {
                if (cur.left != null) {
                    tail.next = cur.left;
                    tail = tail.next;
                }
                if (cur.right != null) {
                    tail.next = cur.right;
                    tail = tail.next;
                }
                cur = cur.next;
            }
            cur = dummy.next;
        }
        return root;
    }
}