LeetCode1104-二叉树寻路

发表于 | 分类于

题目链接

英文链接：https://leetcode.com/problems/path-in-zigzag-labelled-binary-tree/

中文链接：https://leetcode-cn.com/problems/path-in-zigzag-labelled-binary-tree/

题目详述

在一棵无限的二叉树上，每个节点都有两个子节点，树中的节点 逐行 依次按 “之” 字形进行标记。

如下图所示，在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序进行标记；

而偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序进行标记。

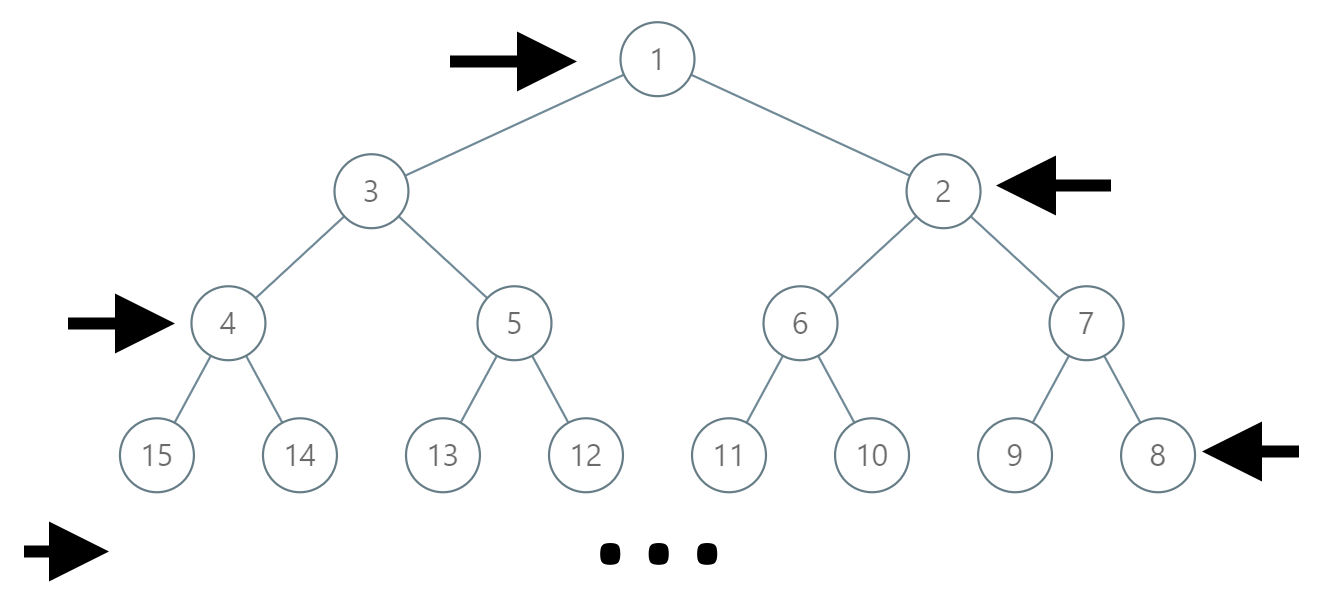
给你树上某一个节点的标号 label，请你返回从根节点到该标号为 label 节点的路径，该路径是由途经的节点标号所组成的。

示例 1：

1
2
输入：label = 14
输出：[1,3,4,14]

示例 2：

1
2
输入：label = 26
输出：[1,2,6,10,26]

提示：

  • 1 <= label <= 10^6

题目详解

  • 二叉树每一层的结点个数增加都是 2 的幂，故可能与位运算相关。
  • 容易发现，如果确定了某一个结点的相对位置（即当前层从左往右数的位置），那么上一层的相对位置为当前层的相对位置除以 2。
  • 因此我们应该根据每一层的相对位置之间的关系来迭代，在这个过程中要根据相对位置得到 label。
  • 以 14 为例，它的二级制为 1110，它的相对位置原本为 110，由于是之字形，实际相对位置为 1111 - 1110 = 1，传到上一层的相对位置为 1 >> 1 = 0，则上一层的 label = 100 + 0 = 100，即为 4。
  • 14 完整递推如下：
    • 初始为 1110，label = 14。
    • 1111 - 1110 = 1, 1 >> 1 = 0, 100 + 0 = 100，lable = 4。
    • 111 - 100 = 11, 11 >> 1 = 1, 10 + 1 = 11，label = 3。
    • 11 - 11 = 0, 0 >> 1 = 0, 1 + 0 =1，label = 1，到达 1 停止。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class LeetCode_01104 {

    public List<Integer> pathInZigZagTree(int label) {
        List<Integer> res = new ArrayList<>();
        int n = Integer.highestOneBit(label);
        while (label > 0) {
            res.add(label);
            int pos = ((n << 1) - 1 - label) >> 1;
            label = (n >> 1) + pos;
            n >>= 1;
        }
        Collections.reverse(res);
        return res;
    }
}