LeetCode304-仅仅反转字母

发表于 | 分类于

题目链接

英文链接：https://leetcode.com/problems/range-sum-query-2d-immutable/

中文链接：https://leetcode-cn.com/problems/range-sum-query-2d-immutable/

题目详述

给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2)。

上图子矩阵左上角 (row1, col1) = (2, 1) ，右下角(row2, col2) = (4, 3)，该子矩形内元素的总和为 8。

示例:

1
2
3
4
5
6
7
8
9
10
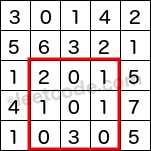
11
给定 matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

说明:

  • 你可以假设矩阵不可变。
  • 会多次调用 sumRegion 方法。
  • 你可以假设 row1 ≤ row2 且 col1 ≤ col2。

题目详解

类似于 二维区域和检索 - 矩阵不可变，也是求出前缀和（左上角到当前点矩形区域），然后做减法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class LeetCode_00304 {

    class NumMatrix {
        private int[][] sums;

        public NumMatrix(int[][] matrix) {
            if (matrix.length == 0 || matrix[0].length == 0) {
                return;
            }
            int m = matrix.length;
            int n = matrix[0].length;
            sums = new int[m + 1][n + 1];
//            for (int i = 1; i <= m; ++i) {
//                for (int j = 1; j <= n; ++j) {
//                    sums[i][j] = sums[i][j - 1] + matrix[i - 1][j - 1];
//                }
//            }
//            for (int j = 1; j <= n; ++j) {
//                for (int i = 1; i <= m; ++i) {
//                    sums[i][j] += sums[i - 1][j];
//                }
//            }
            for (int i = 1; i <= m; ++i) {
                for (int j = 1; j <= n; ++j) {
                    sums[i][j] = sums[i][j - 1] + sums[i - 1][j] - sums[i - 1][j - 1] + matrix[i - 1][j - 1];
                }
            }
        }

        public int sumRegion(int row1, int col1, int row2, int col2) {
            return sums[row2 + 1][col2 + 1] - sums[row2 + 1][col1] - sums[row1][col2 + 1] + sums[row1][col1];
        }
    }
}